Solved Questions on Playing with Numbers
1. What is the difference between P and Q in the given problem?

a) 0
b) −1
c) −2
d) 2
Answer: b) −1
Explanation: The value of P should be between 1 and 9 to satisfy the multiplication. Further, the multiplication is performed as follows:
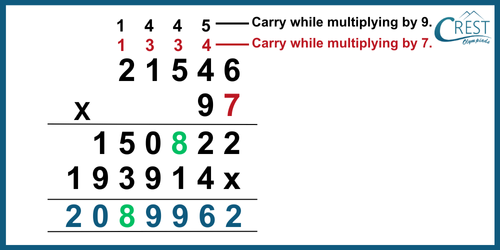
Difference between P and Q in the given problem = 7 − 8 = −1
2. What is the value of a, b and c in the following expression?
a75 – 372 + 72b – 365 + 9c2 = 1801
a) a = 4, b = 1, c = 8
b) a = 4, b = 2, c = 8
c) a = 8, b = 1, c = 4
d) a = 8, b = 2, c = 4
Answer: c) a = 8, b = 1, c = 4
Explanation: The arithmetical operations are shown as:
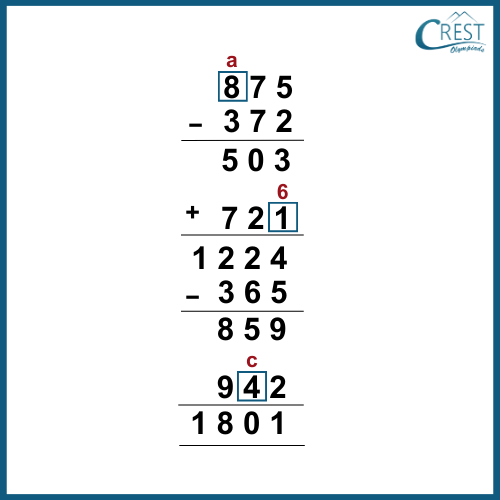
Use the hit-and-trial method to perform operations,
875 – 372 + 721 – 365 + 942 = 1801
Hence, a = 8, b = 1, c = 4
3. If 57AB91 is divisible by 11, then which of the following relationships between A and B is true?
a) A = B − 5 or A = − 6 − B
b) B = A − 5 or A = − 6 − B
c) A = B − 5 or A = − 6 + B
d) B = A − 5 or A = − 6 + B
Answer: d) B = A − 5 or A = − 6 + B
Explanation: A number ‘57AB91’ is divisible by 11 if the difference between the sum of digits at odd places and even places should be either 0 or divisible by 11.
Sum of digits at odd places = 5 + A + 9 = 14 + A
Sum of digits at even places = 7 + B + 1 = 8 + B
Difference = (14 + A) − (8 + B)
= 14 + A − 8 − B
= 6 + A − B
If the difference is 0, then
⇒ 6 + A − B = 0
⇒ A − B = − 6
Hence, A = − 6 + B
OR
If the difference is 11, then
6 + A − B = 11
⇒ A − B = 11 − 6
⇒ A − B = 5
⇒ A = 5 + B
Hence, B = A − 5
4. In a two-digit number, the sum of the digits is 11. If the difference between a number and the number obtained by reversing the digits is 27, then what is the number?
a) 37
b) 47
c) 73
d) 74
Answer: d) 74
Explanation: In a two-digit number, let the ten’s digit be x and the unit’s digit be y.
Number (xy) = 10x + y
By reversing the order of the digits,
Unit’s digit = x and ten’s digit = y
Reversed number (yx) = 10y + x
Sum of a two-digit number = 11
⇒ x + y = 11 …………………………...(i)
Difference between a two-digit number and the number obtained by reversing the digits is 27.
⇒ (10x + y) − (10y + x) = 27
⇒ 10x + y − 10y − x = 27
⇒ 9x − 9y = 27
⇒ 9(x − y) = 27
⇒ x − y = 3 …………………………...(ii)
Adding (i) and (ii),
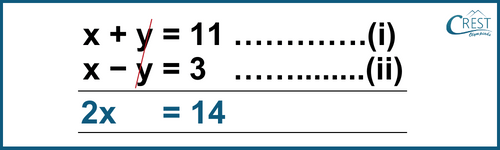
∴ x = 7
Using (i),
x + y = 11
⇒ 7 + y = 11
⇒ y = 11 − 7
∴ y = 4
Hence, Number = 10x + y = 10 × 7 + 4 = 70 + 4 = 74
5. In a three-digit number, the sum of a hundred’s place digit and a unit’s place digit is 7. The ten’s place digit is two-fifths of a hundred place digit. If the difference between a three-digit number and a number obtained by reversing the digits is 297, what is the number obtained by reversing the digits?
a) 225
b) 522
c) 235
d) 532
Answer: a) 225
Explanation: In a three-digit number, let the hundred’s digit be x, ten’s digit be y and the unit’s digit be z.
Number (xyz) = 100x + 10y + z
By reversing the order of the digits,
Hundred’s digit = z
Ten’s digit = y
Unit’s digit = x
Reversed number (zyx) = 100z + 10y + x
Sum of the hundred’s digit and the unit’s digit is 7.
⇒ x + z = 7…………..(i)
Difference between a three-digit number and a number obtained by reversing the digits
⇒ 100x + 10y + z − (100z + 10y + x ) = 297
⇒ 100x + 10y + z − 100z − 10y − x = 297
⇒ 99x − 99z = 297
⇒ 99(x − z) = 297
⇒ x − z = 3 ……………(ii)
Using the elimination method,
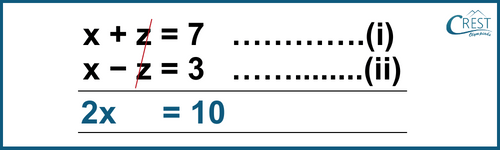
∴ x = 5
Using (ii),
x − z = 3
⇒ z = x − 3
⇒ z = 5 − 3
∴ z = 2
The ten’s place digit is two-fifths of a hundred place digit.
⇒ y = 2⁄5 × x
⇒ y = 2⁄5 × 5
⇒ y = 2
Number (xyz) = 522
Reversed number (zyx) = 225
The number obtained by reversing the digits is 225.






