Solved Questions on Practical Geometry (Constructions)
1. Which is the incorrect option for constructing a quadrilateral DEFG?
a) DE = 3.9 cm, EF = 4.5 cm, GF = 5.2 cm, GE = 4.7 cm and DF = 7.4 cm
b) DE = 3.9 cm, EF = 4.5 cm, GE = 4.7 cm, EG = 6.9 cm and DF = 7.4 cm
c) DE = 3.9 cm, EF = 4.5 cm, GE = 4.7 cm, ∠FED = 37.5° and ∠GEF = 75°
d) DE = 3.9 cm, EF = 4.5 cm, GE = 4.7 cm, ∠FED = 37.5° and ∠EFG = 75
Answer: c) DE = 3.9 cm, EF = 4.5 cm, GE = 4.7 cm, ∠FED = 37.5° and ∠GEF = 75°
Explanation: You should know the given parts of a quadrilateral DEFG:
a) The lengths of all four sides and one diagonal.
DE = 3.9 cm, EF = 4.5 cm, GF = 5.2 cm, GE = 4.7 cm and DF =7.4 cm
b) The lengths of three sides and the lengths of both diagonals.
DE = 3.9 cm, EF = 4.5 cm, GE = 4.7 cm, EG = 8.5 cm and DF = 7.4 cm
d) The lengths of three sides and the two angles.
DE = 3.9 cm, EF = 4.5 cm, GE = 4.7 cm, ∠FED = 47.5° and ∠EFG = 75°
The incorrect statement for constructing a quadrilateral DEFG is:
c) DE = 3.9 cm, EF = 4.5 cm, GE = 4.7 cm, ∠FED = 47.5° and ∠GEF = 75°
∠GEF is a part of ∠FED. Therefore, ∠GEF is smaller than ∠FED.
But here, ∠GEF is greater than ∠FED which is incorrect.
It is shown in the following rough sketch of a quadrilateral DEFG.
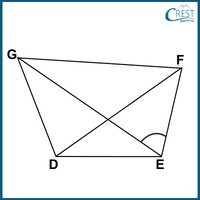
2. Which of the following quadrilateral PQRS is constructed if only one of its sides is given?
a) Kite
b) Parallelogram
c) Rhombus
d) Square
Answer: d) Square
Explanation: A square PQRS is constructed if only one of its sides is given. The length of each side is equal and each angle is right angle.
The sketch of a square PQRS is constructed as follows:
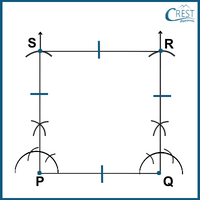
3. Arrange the steps correctly for constructing a parallelogram ABCD.
1) From the point C, draw a line parallel to side AB. This can be done by measuring the distance from point A to point C and transferring that distance to the right or left of point C.
2) Use a ruler to connect points B and D. Hence, parallelogram ABCD is constructed.
3) Using a compass, measure the length of side AB. Without changing the compass width, place the compass on point B and draw an arc that intersects the extension of side AB. Label this point of intersection as C.
4) Draw a line segment to represent one side of the parallelogram ABCD. Label the vertices as A and B.
5) Place the compass on point A and measure the length of side AB. Without changing the compass width, draw an arc from point B. Label the point of intersection on the parallel line as D.
a) 4, 1, 5, 2, 3
b) 4, 1, 5, 3, 2
c) 4, 3, 1, 5, 2
d) 4, 2, 1, 5, 3
Answer: c) 4, 3, 1, 5, 2
Explanation: Constructing a parallelogram ABCD involves specific steps to ensure that opposite sides are parallel and equal in length.
1) Draw a line segment to represent one side of the parallelogram. Label the vertices as A and B.
2) Using a compass, measure the length of side AB. Without changing the compass width, place the compass on point B and draw an arc that intersects the extension of side AB. Label this point of intersection as C.
3) From point C, draw a line parallel to side AB. This can be done by measuring the distance from point A to point C and transferring that distance to the right or left of point C.
4) Place the compass on point A and measure the length of side AB. Without changing the compass width, draw an arc from point B. Label the point of intersection on the parallel line as D.
5) Use a ruler to connect points B and D. Hence, parallelogram ABCD is constructed.
The sketch of a parallelogram ABCD is constructed as follows:
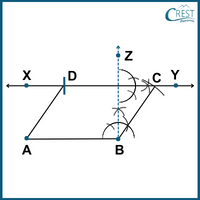
4. Which of the following are NOT the correct steps in the construction of a trapezium KING?
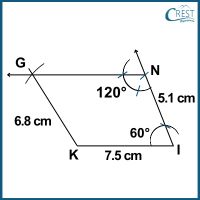
The steps for constructing a trapezium are as follows:
1) Draw a line segment KI of length 7.5 cm.
2) Construct ∠I with a measurement of 60°.
3) From point I, create an arc with a radius of 5.1 cm and cut on the ray passing through point I. Mark the point formed as G.
4) Construct ∠N with a measure of 120°.
5) Draw an arc from point K with a radius of 6.3 cm that intersects at point G. Connect points K and G to complete the trapezium.
a) 2, 4
b) 3, 4
c) 3, 5
d) 4, 5
Answer: c) 3, 5
Explanation: ⇒ The correct steps for constructing a trapezium are as follows:
1) Draw a line segment KI of length 7.5 cm.
2) Construct ∠I with a measurement of 60°.
3) From point I, create an arc with a radius of 5.1 cm and cut on the ray passing through point I. Mark the point formed as N.
4) Construct ∠N with a measure of 120°.
5) Draw an arc from point K with a radius of 6.8 cm that intersects at point G. Connect points K and G to complete the trapezium.
5. Which is the following options is true for the constructed figure JACK?
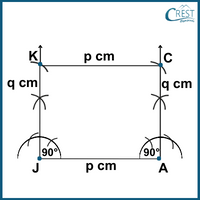
a) The length of each diagonal is the square root of the sum of p and q.
b) The length of each diagonal is the square root of the sum of squares of a and q.
c) If the two diagonals bisect each other at right angles, then the given figure will be a rhombus.
d) The diagonals bisect each other at different angles. One is acute and another one is an obtuse angle.
Answer: d) The diagonals bisect each other at different angles. One is acute and another one is an obtuse angle.
Explanation: The figure of the construction is a rectangle. The properties are as follows:
1) The length of each diagonal is the square root of the sum of squares of p and q.
2) If the two diagonals bisect each other at right angles, then the rectangle is known as a square.
3) The diagonals bisect each other at different angles. One is acute and another one is an obtuse angle.
Only option (d) is the correct statement for a rectangle.






