Solved Questions on Mensuration
1. What is the area of a square PQRS if the length of QS is 8.6 cm?
a) 36.98 cm2
b) 64.98 cm2
c) 73.96 cm2
d) 96.98 cm2
Answer: a) 36.98 cm2
Explanation: A square PQRS with diagonal QS is shown as:
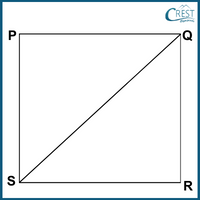
Length of diagonal QS = 8.6 cm
⇒ a√2 = 8.6 cm [Diagonal (d) of a square = a√2]
⇒ a = 8.6/√2 cm
Area of a square = a2
= (8.6/√2)2
= (8.6)2/2
= (8.6 × 8.6)/2
= 36.98 cm2
2. The cuboidal hall is 7.2 metres long, 5 metres broad and 3.5 metres high. If it costs $0.25 to whitewash 1 dm2, what is the cost of whitewashing the four walls and the ceiling?
a) $3015
b) $3025
c) $3035
d) $3045
Answer: c) $3035
Explanation: Area of four walls of a cuboidal hall + Area of a ceiling of a cuboidal hall
= 2(l + b)h + lb
= [2 × (7.2 + 5) × 3.5] + [7.2 × 5]
= [2 × 12.2 × 3.5] + [7.2 × 5]
= 85.4 + 36
= 121.4 m2
= 121.4 m2 × 100 [1 m2 = 100 dm2]
= 12140 dm2
Costs of whitewash 1 dm2 = $0.25
Costs of whitewash 12140 dm2 = $0.25 × 12140 dm2
= $3035
3. An aluminium pipe 16.1 m long has an outer radius of 6.5 cm and an inner radius of 4.5 cm. What is the volume of aluminium used to make the pipe?
a) 0.11132 m3
b) 1.11320 m3
c) 11.1320 m3
d) 111.320 m3
Answer: a) 0.11132 m3
Explanation: Pipe is cylinder in shape.
Height of a pipe = 16.1 m
= (161/10) × 100 cm [1 m = 100 cm]
= 1610 cm
Outer radius = 6.5 cm
Inner radius = 4.5 cm
Volume of aluminum used to make the pipe = outer volume − inner volume
= πR2h − πr2h
= π(R2 − r2)h
= 22⁄7 × [(6.5)2 − (4.5)2] × 1610
= 22⁄7 × [(6.5 + 4.5)(6.5 − 4.5)] × 1610
= 22⁄7 × (11 × 2) × 1610
= 22⁄7 × 22 × 1610
= 484 × 230
= 111320 cm3
= 111320 × 1 cm × 1 cm × 1 cm
= 111320 × 1⁄100 m × 1⁄100 m × 1⁄100 m
= 0.111320 m3
4. What is the area of an isosceles triangle in square metres if an altitude drawn to the base of a triangle is 30 cm and the perimeter is 80 cm.
a) 0.003 m3
b) 0.03 m3
c) 0.30 m3
d) 3 m3
Answer: b) 0.03 m3
Explanation: An isosceles triangle ABC is shown as
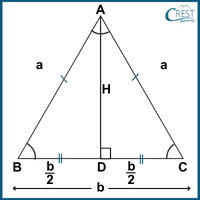
Base (b) of an isosceles triangle = 30 cm
Perimeter of an isosceles triangle = 80 cm
⇒ 2a + b = 80
⇒ 2a + 30 = 80
⇒ 2a = 80 − 30
⇒ 2a = 50
⇒ a = 25 cm
In △ABD,
Using Pythagoras theorem,
Area of a triangle = ½ × b × h
= ½ × 30 × 20
= 300 cm2
= 300 × 1 cm × 1 cm
= 300 × (1÷100)m × (1÷100)m [1 cm = 1/100 m]
= 0.03 m3
5. The difference between two parallel sides of a trapezium is 7 cm. What are the lengths of the parallel sides if the area of the trapezium is 402.5 cm2 and the perpendicular distance between them is 17.5 cm?
a) 17.5 cm and 26.5 cm
b) 17.5 cm and 27.5 cm
c) 19.5 cm and 26.5 cm
d) 19.5 cm and 27.5 cm
Answer: c) 19.5 cm and 26.5 cm
Explanation: The trapezium with parallel sides is shown as
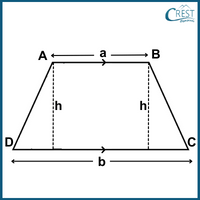
Let smaller side be a cm.
Difference between two parallel sides of a trapezium = 7 cm
⇒ b − a = 7
⇒ b = a + 7
Perpendicular distance between them = h = 17.5 cm
Area of the trapezium = 402.5 cm2
⇒ ½ × (Sum of parallel sides) × height = 402.5
⇒ ½ × (a + b) × h = 402.5
⇒ ½ × (a + a + 7) × 17.5 = 402.5
⇒ 2a + 7 = (402.5 × 2) ÷ 17.5
⇒ 2a + 7 = 46
⇒ 2a = 46 − 7
⇒ 2a = 39
⇒ a = 39/2
⇒ a = 19.5 cm
Therefore, b = a + 7 = 19.5 + 7 = 26.5 cm
Lengths of the parallel sides of the trapezium are 19.5 cm and 26.5 cm.




