Worksheet on Understanding Quadrilaterals for Class 8

Solved Questions on Understanding Quadrilaterals

1. Which of the regular polygons is formed if the exterior angle of a regular polygon is two-thirds of its interior angle?

a) Quadrilateral
b) Pentagon
c) Hexagon
d) Octagon

Answer: b) Pentagon

Explanation: Let the measure of each interior angle be x°.

An exterior angle of a regular polygon is two-thirds of its interior angle.

According to the question,

An exterior angle of a regular polygon = ²⁄₃ × Measure of each interior angle
                                                         = ²⁄₃ x°

Interior angle + exterior angle = 180°
⇒ x° + ²⁄₃  x° = 180°
⇒ 5/3  × x° = 180° 
⇒ x° = 180° × ³⁄₅
⇒ x° = 108°

Therefore, each interior angle is 108°.
⇒ (n − 2) × 180°/n = 108°
⇒ (n − 2) × 180°  = 108° × n
⇒ 180n − 360 = 108n
⇒ 180n − 108n = 360
⇒ 72n = 360
⇒ n = 360/72
⇒ n = 5 sides

The regular polygon is a pentagon.

2. What is the length of each side of the parallelogram PQRS if the length of QR is 11.4 cm and its perimeter is 57.5 cm?

a) PQ = 17.35 cm, QR =  11.4 cm, RS = 17.15 cm and SP =  11.4 cm 
b) PQ = 17.35 cm, QR =  11.4 cm, RS = 17.25 cm and SP =  11.4 cm 
c) PQ = 17.35 cm, QR =  11.4 cm, PS = 17.35 cm and SP =  11.4 cm 
d) PQ = 17.35 cm, QR =  11.4 cm, RS = 17.35 cm and SP =  11.4 cm 

Answer: d) PQ = 17.35 cm, QR =  11.4 cm, RS = 17.35 cm and SP =  11.4 cm 

Explanation: Opposite sides of a parallelogram are of the same length.

PQ = RS and QR = SP
QR = SP = 11.4 cm

Perimeter of parallelogram PQRS = 57.5 cm
⇒ PQ + QR + RS + SP = 57.5 cm
⇒ PQ + 11.4 + PQ + 11.4 = 57.5
⇒ 2PQ + 22.8 = 57.5
⇒ 2PQ = 57.5 − 22.8
⇒ 2PQ = 34.7
⇒ PQ = 34.7/2
⇒ PQ = 17.35 cm
PQ = RS = 17.35 cm

Therefore, the sides of parallelogram PQRS are:
PQ = 17.35 cm, QR = 11.4 cm, RS = 17.35 cm and SP = 11.4 cm

3. The following figure is a rectangle PQRS in which x : y = 2.5 : 3.5. What is the value of 3x−2y ?

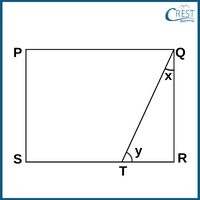
a) 7¹⁄_2^°
b) 15¹⁄_2^°
c) 22¹⁄_2^°
d) 27¹⁄_2^°

Answer: a) 7¹⁄_2^°

Explanation: Let x = 2.5a and y = 3.5a

All angles of a rectangle are 90°.

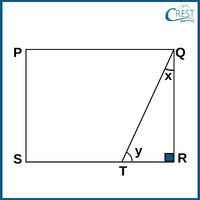
In △QRT,

∠RQT + ∠RTQ + ∠QRT = 180°
⇒ x + y + 90° = 180°
⇒ 2.5a + 3.5a = 180° − 90°
⇒ 6a = 90°
⇒ a = 15°

x = 2.5a = 2.5 × 15° = 37.5°  
y = 3.5a = 3.5 × 15° = 52.5°
3x−2y = 3 × 37.5°−2 × 52.5°
             = 112.5° − 105°
              = 7.5°  
               = 7¹⁄_2^°

4. Which of the following options is NOT true?

a) A rectangle becomes a square if its diagonals intersect each other at a right angle.
b) The diagonals of a rectangle meet at a perpendicular angle.
c) The diagonals of a rhombus meet at a perpendicular angle.
d) The diagonals of an isosceles trapezium are equal in length.

Answer: b) The diagonals of a rectangle meet at a perpendicular angle.

Explanation: The diagonals of a rectangle don’t meet at a perpendicular angle.

5. If ∠A : ∠T = ³√27 : √25, ∠B = (x√225 − 13)° and ∠O =  (x ³√125 + 43)°, then what are the values of all the angles of the trapezium BOAT?

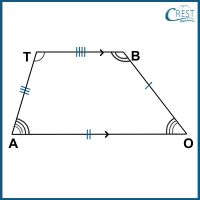
a) ∠B =  89.5°, ∠O = 80.5°, ∠A = 57.5° and ∠T = 112.5°
b) ∠B =  89.55°, ∠O = 80.5°, ∠A = 67.5° and ∠T = 112.5°
c) ∠B =  99.5°, ∠O = 80.5°, ∠A = 57.5° and ∠T = 112.5°
d) ∠B =  99.5°, ∠O = 80.5°, ∠A = 67.5° and ∠T = 112.5°

Answer: d) ∠B = 99.5°, ∠O = 80.5°, ∠A = 67.5° and ∠T = 112.5° 

Explanation: ∠A : ∠T = ³√27 : √25

Let ∠A = ³√27 a = 3a

∠T = √25 a = 5a

In a trapezium BOAT, the sum of each pair of co-interior angles is 180°.

∠A + ∠T = 180°
⇒ 3a + 5a = 180°
⇒ 8a = 180°
⇒ a = 22.5°

∠A = 3a = 3 × 22.5° = 67.5°
∠T = 5a = 5 × 22.5° = 112.5°

∠B = (x √225−13)° = (15x−13)°
∠O = (x  3√125+43)° = (5x+43)°

In a trapezium BOAT, the sum of each pair of co-interior angles is 180°.

∠B + ∠O = 180°
⇒ (15x − 13)° + (5x + 43)° = 180°
⇒ 15x + 5x + 43°−13° = 180°
⇒ 20x + 30° = 180°
⇒ 20x = 150°
⇒ 20x = 150°
⇒ x = 7.5°

∠B = (15x − 13)°
      = (15 × 7.5 − 13)°
      = (112.5 − 13)°
      = 99.5°

∠O = (5x + 43)°
      = (5 × 7.5 + 43)°
      = (37.5 + 43)°
      = 80.5°

All the angles of the trapezium BOAT are:

∠B =  99.5°, ∠O = 80.5°, ∠A = 67.5° and ∠T = 112.5°