Solved Questions on Circle
1. How many circle/circles that passes/pass through three given non-collinear points?
a) 0
b) 1
c) 2
d) 3
Answer: b) 1
Explanation: There is only one circle that passes through three given non-collinear points.
In the figure, A, B and C are non-collinear points (points not in a straight line).
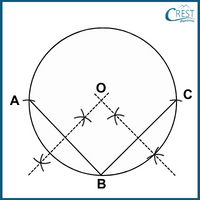
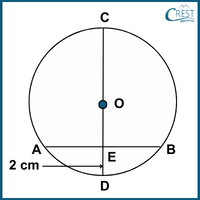
2. What is the radius of the circle if OE bisects the chord AB, the length of ED is 2 cm and the length of chord AB is 10 cm?
a) 5 ½ cm
b) 7 ½ cm
c) 12 ½ cm
d) 14 ½ cm
Answer: d) 14 ½ cm
Explanation: AB = 10 cm [Given : Length of chord AB]
AE = EB = AB/2 = 10/2 = 5 cm [OE bisects the chord]
ED = 2 cm [Given]
Let the radius of the circle be r cm.
OA = OD = r cm
.. OE = OD − ED = (r − 2) cm
From the theorem, the line drawn through the centre of a circle to bisect a chord is perpendicular to the chord.
∠OEA = 90°
The labelled figure is shown as:
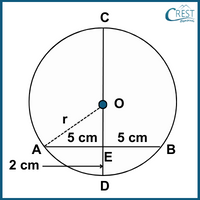
In a right angle triangle AOE, using Pythagoras' theorem:
OA2 = OE2 + AE2
⇒ r2 = (r − 2)2 + 52
⇒ r2 = r2 − 2r + 4 + 52
⇒ r2 − r2 + 2r = 4 + 25
⇒ 2r = 29
⇒ r = 29/2
∴ r = 14 ½ cm
3. Which of the following statements is NOT necessarily true?
Statement A: If two arcs of a circle are congruent, their corresponding chords are equal.
Statement B: If two chords of a circle are equal, their corresponding arcs are equal.
Statement C: Two arcs subtend equal angles at the centre if the arcs are congruent.
Statement D: Two circles are congruent if and only if they have equal radii.
a) A
b) B
c) C
d) D
Answer: b) B
Explanation:
Statement A: If two arcs of a circle are congruent, their corresponding chords are equal. This statement is true. If two arcs are congruent, it means they have the same measure. Since the arc is determined by the central angle subtended by it, the chords corresponding to these arcs will have the same length.
Statement B: If two chords of a circle are equal, their corresponding arcs are equal. This statement is not necessarily true.
Statement C: Two arcs subtend equal angles at the centre if the arcs are congruent. This statement is true. Congruent arcs subtend equal central angles at the centre of the circle.
Statement D: Two circles are congruent, if and only if they have equal radii. This statement is true.
4. Which of the following options is NOT true if AB and CD are two equal chords of a given circle?
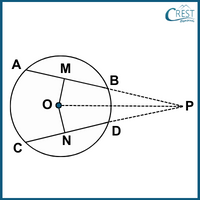
a) PA = PC
b) PB = PD
c) ∠OMP = ∠ONP
d) OA = ON
Answer: d) OA = ON
Explanation: From the theorem, the line drawn through the centre of a circle to bisect a chord is perpendicular to the chord.
Draw OM is perpendicular to AB.
Similarly, ON is perpendicular to CD.
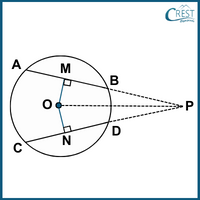
AM = MB [From the theorem, the perpendicular from the centre of a circle to a chord bisects the chord.]
→ AM = MB = CN = ND = ½ AB = ½ CD [Given: AB = CD]
In △MOP and △NOP,
∠OMP = ∠ONP [This statement is true.]
[OM is perpendicular to AB and ON is perpendicular to CD ]
OP = OP [Common side in both triangles △MOP and △NOP]
OM = ON [Equal chords are equidistant from the centre.]
△MOP ≅ △NOP [RHS]
MP = NP [Corresponding parts of congruent triangles are congruent.]
AM = CN [Given: AB = CD]
AM + MP = CN + NP [Adding]
PA = PC [This statement is true.]
MP = NP
MB = ND
MP − MB = NP − ND [Subtracting]
PB = PD [This statement is true.]
The length of OA is the radius and the length of ON is less than the radius. Hence, OA is not equal to ON.
5. Which of the following is NOT correct if these two circles are congruent?
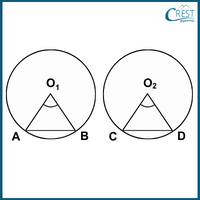
a) The length of AB is equal to the length of CD.
b) ∠AO1B is equal to ∠CO2D.
c) The length of O1A is equal to the length of O2D.
d) The length of arc A1B is equal to the length of arc C2D.
Answer: d) The length of arc A1B is equal to the length of arc C2D.
Explanation: If the two circle are congruent, then the length of AB is equal to the length of CD, ∠AO1B is equal to ∠CO2D, the length of O1A is equal to the length of O2D and the length of arc AB is equal to the length of arc CD.
Hence, The length of arc A1B is equal to the length of arc C2D is not correct.







