Worksheet on Coordinate Geometry for Class 9

Solved Questions on Coordinate Geometry

1. Without actually plotting the points, determine the quadrant of the point with 19 as an ordinate and −27 as an abscissa.

a) First Quadrant
b) Second Quadrant
c) Third Quadrant
d) Fourth Quadrant

Answer: b) Second Quadrant

Explanation: Point with −27 as an abscissa and 19 as an ordinate is (−27, 19).

Hence, this point (−27, 19) of the type (−, +) lies in the second quadrant.

2. Which of the following points lies on the line y = 2x + 3?

a) (1, 7) 
b) (3, 9) 
c) (4, 6) 
d) (5, 7)

Answer: b) (3, 9)

Explanation: Given equation: y = 2x + 3

We need to put the points (x, y) from the options given above in the equation one by one to check which set of points satisfies the equation.
The set of points which satisfies the equation will be our required answer.

In the point (3, 9), put x = 3 and y = 9 in  y = 2x + 3

LHS = 9
RHS = 2 × 3 + 3
= 6 + 3
= 9
LHS = RHS

Thus point ‘b′ satisfies the equation.

Point (3, 9) lies on the line y = 2x + 3.

3. Which one of the following points has an abscissa that is thirty-seven less than one-fifth of the abscissa of point A and whose ordinate is fifteen more than three-fourths of the ordinate of point B?

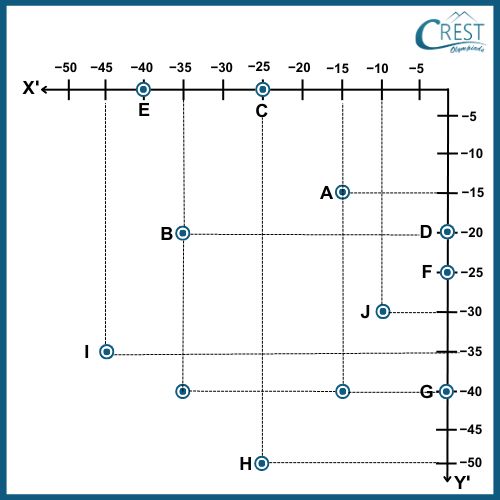
a) D
b) E
c) G
d) H

Answer: b) E

Explanation: From the graph, point A is (−15, −15) and point B is (−35, −20).

The abscissa of A is −15 and the ordinate of B is −20.

The point whose abscissa is thirty-seven less than one-fifth of the abscissa of point A = ⅕ × (−15) − 37
    = −3 − 37
    = −40

The point whose ordinate is fifteen more than three-fourths of the ordinate of point B = ¾ × (−20) + 15
= − 15 + 15
= 0
The point is (−40, 0).
Hence, the point on the graph is E.

4. If the midpoint of the line segment joining the points A (2, 3) and B (k, 5) is Q (x, y) and x + y − 9 = 0, What is the value of k?

a) 6
b) 7
c) 8
d) 9

Answer: c) 8

Explanation: Midpoint of the line segment M joining A (2, 3) and B (k, 5) is shown as:

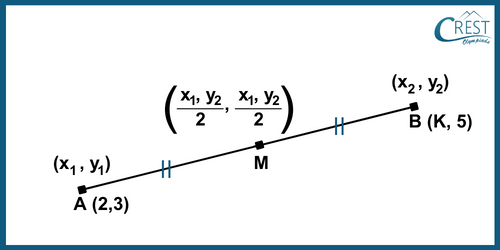
Midpoint M ($\frac{\frac{\mathrm{2\; +\; k}}{}}{\frac{2}{}}$, $\frac{\frac{\mathrm{3\; +\; 5}}{}}{\frac{2}{}}$) = M ($\frac{\frac{\mathrm{2\; +\; k}}{}}{\frac{2}{}}$ , 4)

Also, ($\frac{\frac{\mathrm{2\; +\; k}}{}}{\frac{2}{}}$ , 4) = (x, y)

∴ $\frac{\frac{\mathrm{2\; +\; k}}{}}{\frac{2}{}}$ = x and 4 = y

Also, x + y − 9 = 0 (given)  ……..(i)

Thus, putting the values of x and y in (i) we get,

$\frac{\frac{\mathrm{2\; +\; k}}{}}{\frac{2}{}}$ + 4 − 9 = 0
⇒ $\frac{\frac{\mathrm{2\; +\; k}}{}}{\frac{2}{}}$ = 5
⇒ 2 + k = 10

∴ k = 10 − 2 

= 8

5. The point whose ordinate is nine less than five-sevenths of the ordinate of point S and whose abscissa is twenty-one less than the abscissa of point T. In which quadrant does this point lie?

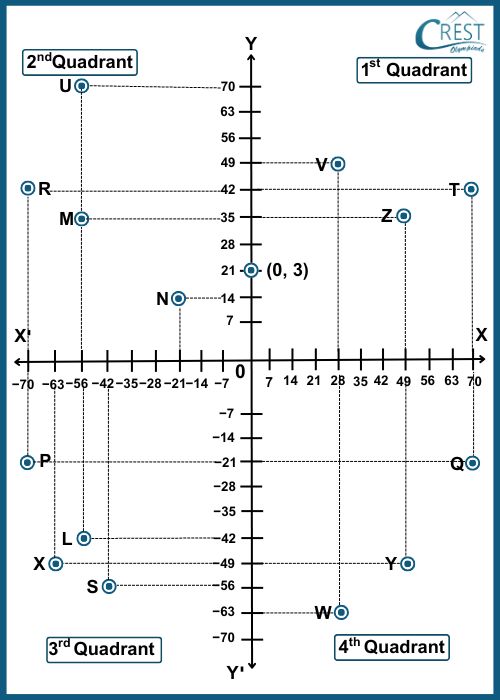
a) Quadrant I
b) Quadrant II
c) Quadrant III
d) Quadrant IV

Answer: d) Quadrant IV

Explanation: From the graph, point S is (−42, −56) and point T is (70, 42).
The ordinate of A is −56 and the abscissa of B is 70.
The point whose ordinate is nine less than five-sevenths of the ordinate of point S
= 5/7 × (−56) − 9
= −40 − 9
= −49

The point whose abscissa is twenty-one less than the abscissa of point T
= 70 − 21
= 49

The point is (49, −49). Therefore, the point on the graph is Y.
Hence, the point lies in the quadrant IV.