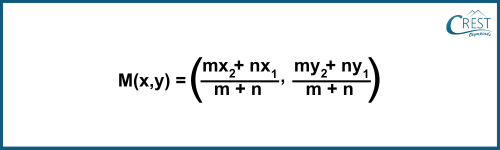Practice Questions on Coordinate Geometry
1. Which type of triangle is formed using the vertices A (1, 2), B (−3, 12) and C (−5, −6)?
a) Isosceles triangle
b) Equilateral triangle
c) Scalene triangle
d) Right-angled triangle
Answer: c) Scalene triangle
Explanation: We know that:
→ An equilateral triangle has all sides equal.
→ An isosceles triangle has two sides equal.
→ A scalene triangle has no sides equal.
→ A right-angled triangle satisfies the Pythagoras Theorem.
We can find the lengths of the sides of a triangle using the distance formula.
Distance between any two points (x1, y1) and (x2, y2) is given by:
d = √[(x2 − x1)2 + (y2 − y1)2]
We are given △ABC with vertices A (1, 2), B (−3, 12) and C (−5, −6).
Now, using the distance formula, find the length of AB, BC and CA.
→ AB = √[((− 3) − 1)2 + (12 − 2)2]
= √[(− 4)2 + (10)2]
= √[16 + 100]
= √116
= 2√29 units
→ BC = √[((− 5) − (− 3))2 + ((− 6) − 12)2]
= √[(− 5 + 3)2 + (− 6 − 12)2]
= √[(− 2)2 + (− 18)2]
= √[4 + 324]
= √328
= 2√82 units
→ CA = √[((− 5) − 1)2 + ((− 6) − 2)2]
= √[(− 6)2 + (− 8)2]
= √[36 + 64]
= √100
= 10 units
Now, AB2 = (√116)2
= 116
BC2 = (√328)2
= 328
CA2 = (10)2
= 100
Thus, AB2 + CA2 ≠ BC2
Thus, it does not satisfy the Pythagoras theorem.
Since the length of all three sides is different and it doesn’t satisfy the Pythagoras theorem, thus △ABC is a scalene triangle.
2. The point which divides the line segment joining the points (5, –9) and (–2, 5) in ratio 2 : 3 internally lies in which quadrant?
a) First quadrant
b) Second quadrant
c) Third quadrant
d) Fourth quadrant
Answer: d) Fourth quadrant
Explanation:Here,
x1 = 5
x2 = − 2
y1 = − 9
y2 = 5
m = 2
n = 3
Let P(x, y) divides the line segment joining the points (5, – 2) and (− 9, 5) in the ratio 2 : 3 internally. Thus the coordinates of P are

3. If the point P(5, 4) lies on the line segment joining points A(3, 2) and B(9, 8), then which of the following is true?
a) BP = AB/3
b) AP = BP/2
c) AP = BP/3
d) BP = AB/2
Answer: b) AP = BP/2
Explanation: We are given that point P(5, 4) lies on the line segment joining points A(3, 2) and B(9, 8).
Thus,
AP = √[(x2 − x1)2 + (y2 − y1)2]
= √[(5 − 3)2 + (4 − 2)2]
= √[(2)2 + (2)2]
= √[4 + 4]
= √8
= 2√2
BP = √[(x2 − x1)2 + (y2 − y1)2]
= √[(5 − 9)2 + (4 − 8)2]
= √[(− 4)2 + (− 4)2]
= √[16 + 16]
= √32
= 4√2
AB = √[(x2 − x1)2 + (y2 − y1)2]
= √[(9 − 3)2 + (8 − 2)2]
= √[(6)2 + (6)2]
= √[36 + 36]
= √72
= 6√2
We know that: AP = 2√2 and BP = 4√2
∴ AP = BP/2
4. Out of the following points, which three points satisfy the condition of collinearity?
a) (5, −3), (4, 1) and (−2, 7)
b) (1, 2), (3, −2) and (0, 5)
c) (−4, −1), (2, 3) and (−3, 6)
d) (−6, 10), (−4, 6) and (3, −8)
Answer: d) (−6,10), (−4, 6) and (3, −8)
Explanation: We know that the area of a triangle formed by three collinear points is zero.
Also, If A (x1, y1), B (x2, y2) and C (x3, y3) are the vertices of a △ABC, then its area is given by:
Area = ½ [x1(y2 − y3) + x2(y3 − y1) + x3(y1 − y2)]
Option a)
We are given three points (5, −3), (4, 1) and (−2, 7)
Here,
x1 = 5
x2 = 4
x3 = −2
y1 = −3
y2 = 1
y3 = 7
Thus, Area of triangle = ½[x1(y2 − y3) + x2(y3 − y1) + x3(y1 − y2)]
= ½[5(1 − 7) + 4(7 − (− 3)) + (− 2)((− 3) − 1)]
= ½[(5)(−6) + 4(10) + (−2)(−4)]
= ½[−30 + 40 + 8]
= ½[18]
= 9
≠ 0
Thus, the points are not collinear.
Option b)
We are given three points (1, 2), (3, −2) and (0, 5)
Here,
x1 = 1
x2 = 3
x3 = 0
y1 = 2
y2 = −2
y3 = 5
Thus, Area of triangle = ½[x1(y2 − y3) + x1(y3 − y1) + x3(y1 − y2)]
= ½[1(− 2 − 5) + 3(5 − 2) + 0(2 − (− 2))]
= ½[1(− 7) + 3(3) + 0(2 + 2)]
= ½[−7 + 9 + 0]
= ½[2]
= 1
≠ 0
Thus, the points are not collinear.
Option c)
We are given three points (−4, −1), (2, 3) and (−3, 6)
Here,
x1 = −4
x2 = 2
x3 = −3
y1 = −1
y2 = 3
y3 = 6
Thus, Area of triangle = ½[x1(y2 − y3) + x2(y3 − y1) + x3(y1 − y2)]
= ½[(−4)(3 − 6) + 2(6 − (−1)) + (−3)((−1) − 3)]
= ½[(− 4)(− 3) + 2(7) + (− 3)(− 4)]
= ½[12 + 14 + 12]
= ½[38]
= 19
≠ 0
Thus, the points are not collinear.
Option d)
We are given three points (− 6, 10), (−4, 6) and (3, −8)
Here,
x1 = −6
x2 = −4
x3 = 3
y1 = 10
y2 = 6
y3 = −8
Thus, Area of triangle = ½[x1(y2 − y3) + x2(y3 − y1) + x3(y1 − y2)]
= ½[(−6)(6 − (−8)) + (−4)(−8 − 10) + 3(10 − 6)]
= ½[(−6)(14) + (−4)(−18) + 3(4)]
= ½[−84 + 72 + 12]
= ½[−84 + 84]
= ½[0]
= 0
So, the area of the triangle is zero. Thus, the points are collinear.
5. In what ratio does the point (–2, 3) divide the line segment joining the points A (–8, 6) and B (5, –9)?
a) 7 : 5
b) 7 : 6
c) 5 : 7
d) 6 : 7
Answer: d) 6 : 7
Explanation: Let point (–2, 3) divide the line segment joining the points A(–8, 6) and B(5, –9) in k : 1 ratio.
We know that if the point M (x, y) divides the line segment joining P (x1, y1) and Q (x2, y2) internally in the ratio m : n, then the coordinates of M are given by the section formula as
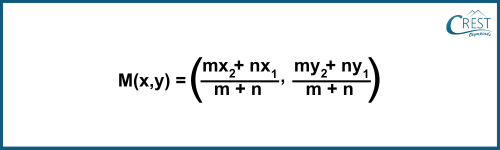
(–2, 3) = (5k - 8/k + 1, - 9k + 6/k + 1)
We know that if (x, y) = (a, b) then x = a and y = b
–2 = (5k - 8/k + 1) and 3 = (-9k + 6/k + 1)
Using –2 = 5k - 8k + 1 to find the ratio.
⇒ –2 = (5k - 8/k + 1)
⇒ –2 (k + 1) = 5k – 8
⇒ –2k – 2 = 5k – 8
⇒ –2k – 5k = – 8 + 2
⇒ –7k = – 6
⇒ 7k = 6
⇒ k = 6/7
Ratio = k : 1 = 6/7 : 1 = 6 : 7
Thus, point (– 2, 3) divide the line segment joining the points A(– 8, 6) and B(5, – 9) in the ratio 6 : 7.