Worksheet on Chapter: Circles and Area Related to Circles - Class 10

Solved Questions based on Circles and Areas related to Circles

1. If three circles, each of radius 10 cm touch each other externally, then what is the approximate area of the shaded portion?

a) 18 cm²
b) 14 cm²
c) 20 cm²
d) 16 cm²

Answer: d) 16 cm²

Explanation: We are given that three circles of radius 10 cm touch each other externally.

Join the centres of each circle.

After joining the centres, we get an equilateral triangle of side 20 cm (since the radius of each circle is 10 cm)

We know that each angle in an equilateral triangle measures 60°.

Thus, we’ll have the figure as shown below

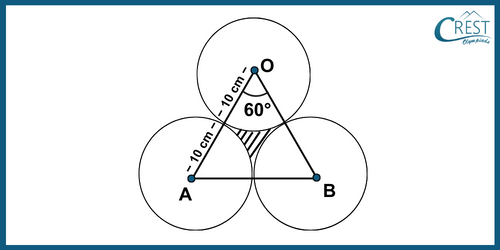
Area of Shaded region = Area of Equilateral Triangle OAB − Area of 3 sectors of angle 60°

We know that

Area of an equilateral triangle = √³⁄₄ × (side)²

Area of the sector of angle θ = ^θ⁄₃₆₀ × πr²

Thus,

Area of Shaded region = Area of Equilateral Triangle OAB − Area of 3 sectors of angle 60°
= √³⁄₄ × (20)² − [3 × ⁶⁰⁄₃₆₀ × ²²⁄₇ × (10)²]
= √³⁄₄ × (400) − [3 × ¹⁄₆ × ²²⁄₇ × 100]
= 100√3 − [¹⁄₂ × ²²⁄₇ × 100]
= (100 × 1.73) − [¹¹⁄₇ × 100] [Since √3 = 1.73]
= 173 − 157 (approx)
= 16 cm² (approx)

Area of shaded region = 16 cm² (approx)

2. AB and CD are two chords towards one side of its centre. AB || CD and the distance between the chords is 1 cm. If AB = 10 cm and CD = 8 cm, then what is the radius of the circle?

a) √42 cm
b) √47 cm
c) √41 cm
d) √43 cm

Answer: c) √41 cm

Explanation: Let O be the centre of the circle.

Let the perpendicular from O cut the chord AB at P and and chord CD at Q respectively. Join OA and OC.

The figure is shown below

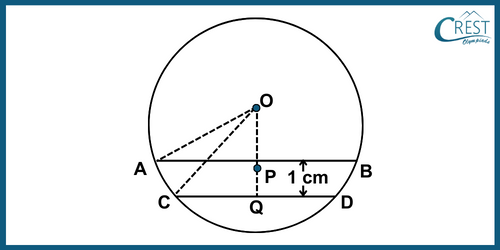
We are given that AB = 10 cm and CD = 8 cm

We know that the perpendicular from the centre of a circle to a chord bisects the chord.

Thus, AB = 2AP and CD = 2CQ

→ AP = 5 cm
→ CQ = 4 cm

Let r be the radius and OP be x cm

In △APO,

Using Pythagoras theorem,

→ (OA)² = (OP)² + (AP)²
→ (r)² = (x)² + (5)²
→ r² = x² + 25 … (1)

In △CQO,

Since PQ = 1 cm

OQ = OP + PQ

→ OQ = x + 1

Using Pythagoras theorem,

→ (OC)² = (OQ)² + (CQ)²
→ (r)² = (x + 1)² + (4)²
→ r² = x² + 2x + 1 + 16
→ r² = x² + 2x + 17 … (2)

From equation (1) and (2)

→ x² + 25 = x² + 2x + 17
→ x² − x² + 25 − 17 = 2x
→ 8 = 2x
→ x = 4 cm

Substitute x = 4 cm in equation (1) to find the value of r

→ r² = (4)² + 25
→ r² = 16 + 25
→ r² = 41
→ r = √41 cm

3. In the given figure, AC is the diameter of the circle. ED is a chord parallel to AC. If ∠CBE = 37°, then what is the value of ∠DEC?

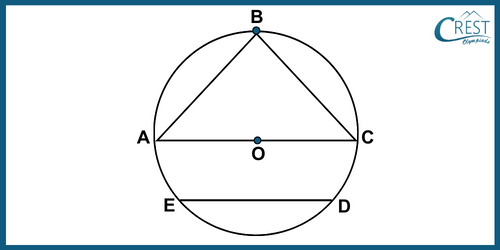
a) 37°
b) 53°
c) 45°
d) 47°

Answer: b) 53°

Explanation: Join AE, BE and CE.

Let ∠DEC be θ.

Consider the figure below,

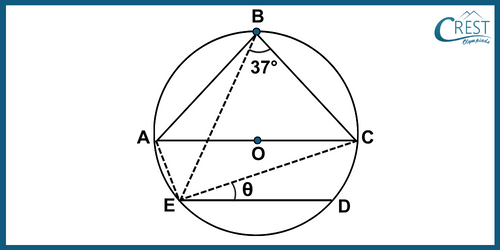
We know that AC is the diameter and an angle in a semicircle is a right angle.

Thus, 

∠ABC = 90°

We are given ∠CBE = 37°

∠ABE = ∠ABC − ∠CBE
         = 90° − 37°
         = 53°

∠ABE = 53°

We know that angles in the same segment of a circle are equal.

∠ABE = ∠ACE = 53°

We are given that AC || ED,

∠ACE = ∠DEC

∠DEC = 53°

4. If the area of a sector of a circle of radius 30 cm is 90 π cm2, then what is the length of the corresponding arc of the sector?

a) 6 π cm
b) 60 π cm
c) 8 π cm
d) 36 π cm

Answer: a) 6 π cm

Explanation: Let the central angle be θ.

We know that 

Area of the sector of angle θ = ^θ⁄₃₆₀ × πr²

→ 90 π = ^θ⁄₃₆₀ × π(30)²
→ 90 = ^θ⁄₃₆₀ × (30)²
→ θ = ^360×90⁄_30×30
→ θ = 36°

We know that the length of an arc of a sector of angle θ = ^θ⁄₃₆₀ × 2πr

Thus, length of the corresponding arc of the sector = ³⁶⁄₃₆₀ × 2π × 30
                                                                          = ¹⁄₁₀ × 60π
                                                                          = 6 π

Length of the corresponding arc of the sector = 6 π cm

5. In the figure, if PA and PB are tangents to the circle with centre O such that ∠APB = 30°, then what is the value of ∠OBA?

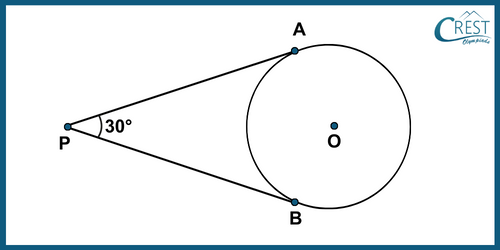
a) 25°
b) 15°
c) 75°
d) 35°

Answer: b) 15°

Explanation: Join OA, OB and AB.

OA and OB are the radius of the circle.

Consider the figure shown below

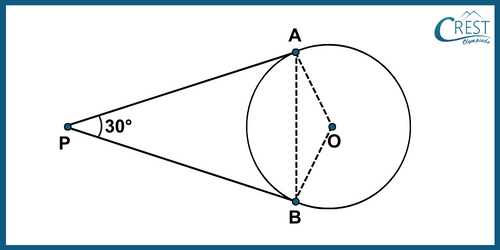
Given PA and PB are the tangents.

We know that the lengths of tangents drawn from an external point to a circle are equal.

→ PA = PB
→ ∠PAB = ∠PBA    [Angles opposite to equal sides are equal]

We know that the sum of all angles of a triangle is 180°.

Thus, in △PAB,

→ ∠PAB + ∠PBA + ∠APB = 180°
→ ∠PAB + ∠PAB + 30° = 180°
→ 2∠PAB = 180° − 30°
→ 2∠PAB = 150°
→ ∠PAB = 150° / 2
→ ∠PAB = ∠PBA = 75° 

We know that the tangent at any point of a circle is perpendicular to the radius through the point of contact.

→ ∠PBO = 90°
→ ∠PBA + ∠OBA = 90°
→ 75° + ∠OBA = 90°
→ ∠OBA = 90° – 75°
→ ∠OBA = 15°