Solved Questions based on Construction
1. Which of the following steps of construction is INCORRECT while constructing a circumscribing circle of an equilateral triangle ABC of side 5 cm?
Step 1: Draw a line segment AB = 5 cm.
Step 2: With A and B as the centres, draw arcs of radius 5 cm intersecting each other at C.
Step 3: Join AC and BC. △ABC is an equilateral triangle.
Step 4: Draw the median of AB and AC that intersect each other at O.
Step 5: Join OA.
Step 6: With O as the centre and OA as the radius, draw a circle passing through A, B and C.
a) Step 2
b) Step 6
c) Step 4
d) Step 3
Answer: c) Step 4
Explanation: Consider the figure given below:
The steps to construct a circumscribing circle of an equilateral triangle ABC of side 5 cm are:
Step 1: Draw a line segment AB = 5 cm.
Step 2: With A and B as the centres, draw arcs of radius 5 cm intersecting each other at C.
Step 3: Join AC and BC. △ABC is an equilateral triangle.
Step 4: Draw the perpendicular bisectors of side AB and AC intersecting each other at O.
Step 5: Join OA.
Step 6: With O as the centre and OA as the radius, draw a circle passing through A, B and C.
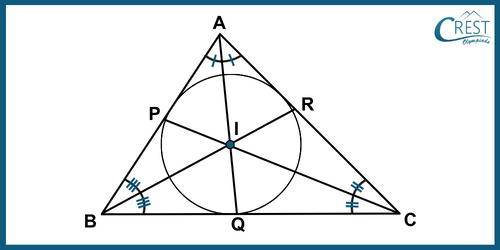
2. If the angle bisectors of angles P and R of a triangle PQR meet at O, then what is the point O called?
a) Centroid
b) Orthocentre
c) Circumcentre
d) Incentre
Answer: d) Incentre
Explanation:
- Incentre: The incentre of a triangle is where the three angle bisectors meet. It is like the centre of a circle that fits inside the triangle perfectly and touches all three sides.
- Circumcentre: The circumcentre is a point where the perpendicular bisectors of the three sides of a triangle intersect. It is the centre of a circle that passes through all three vertices of the triangle.
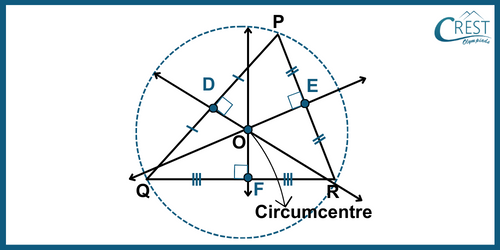
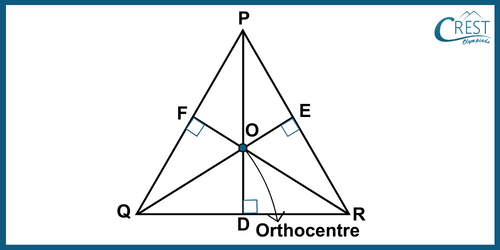
- Orthocentre: The orthocentre is a point where the three altitudes of a triangle intersect. It is where the lines drawn straight up from each corner meet.
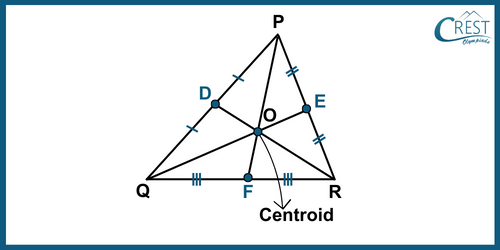
- Centroid: The centroid is a point where the three medians (lines joining each vertex to the midpoint of the opposite side) of a triangle intersect.
3. What is the measure of each internal angle of a regular hexagon?
a) 100°
b) 110°
c) 120°
d) 130°
Answer: c) 120°
Explanation: The interior angle of the regular polygon of n sides is given by:
Each interior angle = × 90°
A regular hexagon has 6 sides.
Thus, n = 6
Each interior angle of a regular hexagon = × 90°
= × 90°
= (12 − 4) × 15°
= 8 × 15°
= 120°
Each interior angle of a regular hexagon = 120°
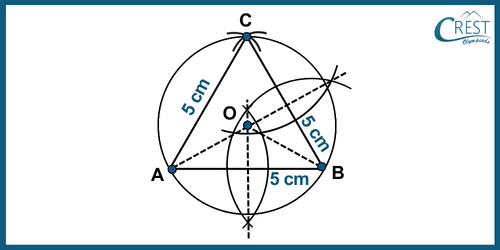
4. What will be the radius of the circle circumscribing an equilateral triangle of side 4.5 cm constructed using a ruler and compass?
a) 2.4 cm
b) 2.6 cm
c) 3.4 cm
d) 3.6 cm
Answer: b) 2.6 cm
Explanation: Construct the figure using the given steps:
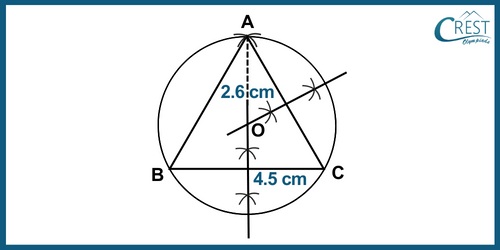
Steps of Construction:
Step 1: Make a line segment BC of length 4.5 cm.
Step 2: Use points B and C as centres and draw two arcs with a radius of 4.5 cm intersecting each other at point A.
Step 3: Join AC and AB.
Step 4: Draw the perpendicular bisectors of AC and BC intersecting each other at O.
Step 5: Using O as the centre and OA, OB or OC as the radius, draw a circle. This circle will pass through points A, B, and C.
Step 6: This is the required circumcircle of triangle ABC. After measuring, the radius is OA is 2.6 cm.
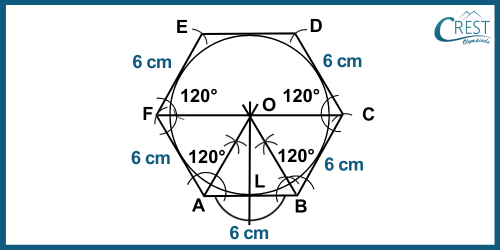
5. Arrange the given steps for constructing an inscribing circle of a regular hexagon of side 6 cm in CORRECT order.
Steps of Construction:
Step 1: At points A and B, draw the angle bisectors of angles A and B intersecting each other at point O.
Step 2: With O as the centre and OL as the radius, draw a circle touching the hexagon's sides.
Step 3: Draw a line segment AB of length 6 cm.
Step 4: From O, draw OL perpendicular to AB.
Step 5: At points F and C, draw rays making an angle of 120° each. These lines cut off segments FE and CD, both measuring 6 cm.
Step 6: Draw rays making an angle of 120° each at points A and B. These lines cut off segments AF and BC, each measuring 6 cm.
Step 7: Join DE. Thus, ABCDEF is the required regular hexagon.
a) 3 - 5 - 6 - 1 - 7 - 4 - 2
b) 3 - 1 - 6 - 5 - 7 - 4 - 2
c) 3 - 6 - 5 - 7 - 1 - 4 - 2
d) 3 - 1 - 5 - 6 - 7 - 4 - 2
Answer: c) 3 - 6 - 5 - 7 - 1 - 4 - 2
Explanation:
Steps of Construction:
Step 1: Draw a line segment AB of length 6 cm.
Step 2: Draw rays making an angle of 120° each at points A and B. These lines cut off segments AF and BC, each measuring 6 cm.
Step 3: At points F and C, draw rays making an angle of 120° each. These lines cut off segments FE and CD, both measuring 6 cm.
Step 4: Join DE. Thus, ABCDEF is the required regular hexagon.
Step 5: At A and B, draw the angle bisectors of angles A and B intersecting each other at point O.
Step 6: From O, draw OL perpendicular to AB.
Step 7: With O as the centre and OL as the radius, draw a circle touching the hexagon's sides. Thus, this circle is the required incircle.
Construct the figure using the given steps: