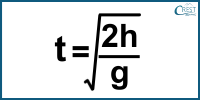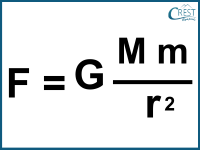1. Two objects are released simultaneously from different heights. If one object takes 2 seconds to reach the ground, how much time will the other object take to reach the ground if its height is four times the height of the first object?
a) 4 s
b) 2 s
c) 8 s
d) 1 s
Answer: a) To solve this question we can use the following equation for free-falling objects:
h = ut + 1/2 g t2
Since the initial velocity u is zero, the equation simplifies to:
h = 1/2 g t2
To find the time t, we rearrange the equation as follows:
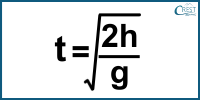
Where:
t is the time of fall,
h is the height from which the object is dropped,
g is the acceleration due to gravity (approximated as 9.8 ms-2)
Let's denote the height of the first object as h1 and the height of the second object as h2, where h2 = 4 x h1
Given that the first object takes 2 seconds to reach the ground, we have:
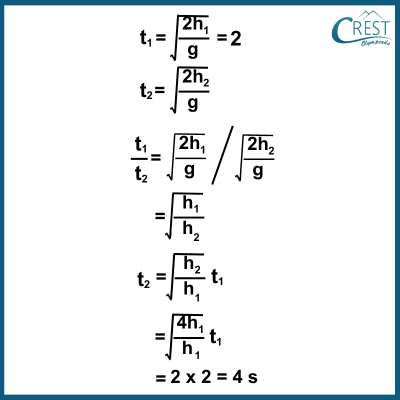
Therefore, the time it will take for the second object to reach the ground is 4 seconds.
2. Consider the following data for three planets:
Planet X: orbital period = 2 years, semi-major axis = 3 AU
Planet Y: orbital period = 5 years, semi-major axis = 5 AU
Planet Z: orbital period = 10 years, semi-major axis = 8 AU
According to Kepler's Third Law, which planet has the shortest orbital period?
a) Planet X
b) Planet Y
c) Planet Z
d) Not enough information to determine
Answer: a) According to Kepler's Third Law, the square of the orbital period (T) is directly proportional to the cube of the semi-major axis (R) of the orbit. Mathematically:
T2 ∝ R3
Let's calculate the ratios for each planet:
For Planet X:
(TX2) / (RX3) = (22) / (33) = 4 / 27
For Planet Y:
(TY2) / (RY3) = (52) / (53) = 25 / 125
For Planet Z:
(TZ2) / (RZ3) = (102) / (83) = 100 / 512
Comparing these ratios, we can see that Planet X indeed has the smallest value of (TX2) / (RX3), which indicates it has the shortest orbital period among the three planets.
3. Consider two planets, X and Y, with the same mass but different radii. If planet X has twice the radius of planet Y, how does the acceleration due to gravity on planet X compare to that on planet Y?
a) The acceleration on planet X is twice that on planet Y
b) The acceleration on planet X is half that on planet Y
c) The acceleration on planet X is one fourth that on planet Y.
d) The acceleration relationship depends on the planets' masses
Answer: c) The acceleration due to gravity is inversely proportional to the square of the distance from the centre of mass. This relationship is described by the formula:
g ∝ 1/r2
Where
g is the acceleration due to gravity and
r is the distance from the centre of mass.
For planet Y, the acceleration due to gravity will be:
gY ∝ 1/rY2
Given that planet X has twice the radius of planet Y (which means the distance r is doubled for planet X compared to planet Y), the acceleration due to gravity on planet X will be:
gX ∝ 1/(2rY)2
gX ∝ 1/4rY2
gXgY = 1/4
Comparing gX and gY, we can see that gX is one-fourth of gY, as indicated in option c.
4. In the following question, you will find an assertion and a reason. Select the appropriate option that applies.
Assertion: The acceleration due to gravity (g) at a depth below the Earth's surface is lower compared to the value of g at the surface.
Reason: The mass of the Earth decreases as an object moves deeper below the surface, leading to a weaker gravitational force.
a) Both the assertion and reason are true, and the reason is the correct explanation of the assertion.
b) Both the assertion and reason are true, but the reason is not the correct explanation of the assertion.
c) The assertion is true, but the reason is false.
d) The assertion is false, but the reason is true.
Answer: c) The assertion that the acceleration due to gravity (g) at a depth below the Earth's surface is lower compared to the value of g at the surface is true.
However, the reason provided – "The mass of the Earth decreases as an object moves deeper below the surface, leading to a weaker gravitational force" – is false. The mass of the Earth remains constant regardless of depth below the surface, and it's the distribution of mass that causes the decrease in gravity at greater depths. The true explanation is related to the distribution of mass, not a decrease in the Earth's overall mass.
5. A spacecraft with a mass of 5000 kg is launched from Earth's surface into outer space. Calculate the weight of the spacecraft on Earth's surface and explain how this weight changes as the spacecraft moves away from Earth.
a) Weight = 50,000 N; Weight decreases as the spacecraft moves away from Earth.
b) Weight = 50,000 N; Weight remains constant as the spacecraft moves away from Earth.
c) Weight = 5000 N; Weight decreases as the spacecraft moves away from Earth.
d) Weight = 5000 N; Weight remains constant as the spacecraft moves away from Earth.
Answer: a) The weight of an object on Earth's surface is the force with which it is attracted towards the centre of the Earth due to gravity. The formula to calculate weight (W) is given by:
W = mg
Where:
m is the mass of the object (5000 kg in this case),
g is the acceleration due to gravity on Earth's surface (9.8 ms-2, or approximately 10 ms-2).
Substitute these values into the formula:
W = 5000 kg × 10 ms-2 = 50,000 N
So, the weight of the spacecraft on Earth's surface is 40,000 N.
As the spacecraft moves away from Earth into outer space, the distance (r) between the spacecraft and the centre of the Earth increases. According to the universal law of gravitation, the force of gravity (F) between two objects is inversely proportional to the square of the distance (r) between their centres:
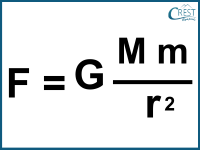
Since weight is the force of gravity on an object, as the spacecraft moves away from Earth, the force of gravity on it decreases. Therefore, the weight of the spacecraft decreases as it moves away from Earth.