Square of a number is the number which is acquired by multiplying the number by itself. Squares with values ranging from 1 to 30 have values from 1 to 900. These numbers assist students in easily simplifying complicated mathematical equations. The exponential form of the squares 1 to 30 is represented as x².

Chart for Squares 1 to 30

Students can learn the values of squares 1 to 30 using square charts and utilize them in calculations. Memorizing these values help students in solving different types of simplification, mensuration problems, quadratic equations, etc. very easily and quickly for CREST Mathematics Olympiad (CMO) and similar competitions. Students can use these values of squares to quickly and effectively solve time-consuming arithmetic problems.

Let's begin learning the values of the square of the numbers 1 to 30, which are split down into three stages, namely square from 1 to 10, square from 11 to 20 and square roots from 21 to 30. Below is the squares table of numbers from 1 to 30.

Squares from 1 to 10

The below chart shows the square values from 1 to 10 -

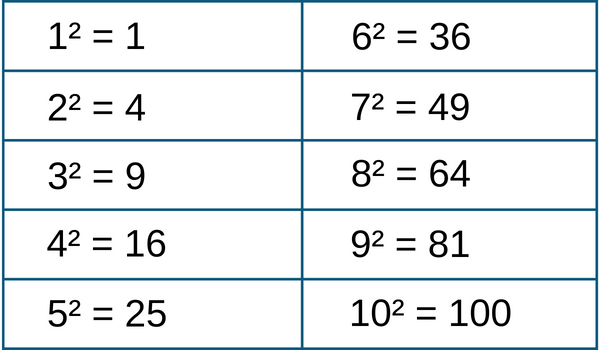
squares-from-1-to-10

Squares from 11 to 20

The below chart shows the square values from 11 to 20 -

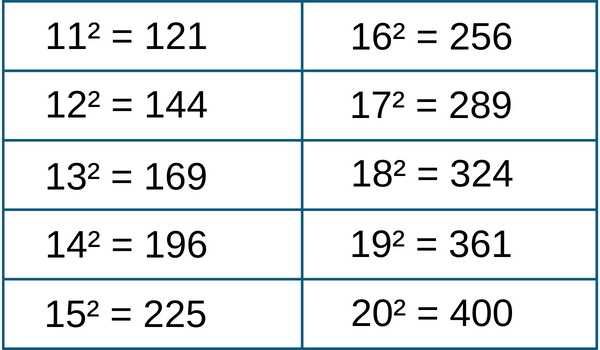
squares-from-11-to-20

Squares from 21 to 30

The below chart shows the square values from 21 to 30 -

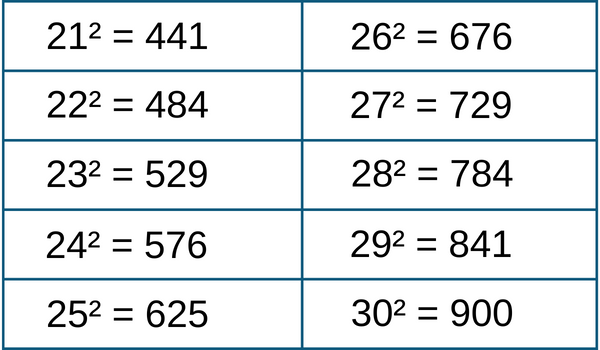
squares-from-21-to-30

Tables of Squares

Students may recognize all perfect squares from 1 to 900 by learning squares 1 to 30. They can also approximately calculate a square root by interpolating between known squares. The table below is a list of the values for squares upto 30.

1² = 1	16² = 256
2² = 4	17² = 289
3² = 9	18² = 324
4² = 16	19² = 361
5² = 25	20² = 400
6² = 36	21² = 441
7² = 49	22² = 484
8² = 64	23² = 529
9² = 81	24² = 576
10² = 100	25² = 625
11² = 121	26² = 676
12² = 144	27² = 729
13² = 169	28² = 784
14² = 196	29² = 841
15² = 225	30² = 900

Squares 1 to 30 - Even Numbers

From numbers 1 to 30 there are a total of 15 even numbers. As we know, even numbers can be expressed in the form of 2n, where n = 1,2,3,4,5,…

The values of squares 1 to 30 for even numbers are listed in the table below.

2² = 4	18² = 324
4² = 16	20² = 400
6² = 36	22² = 484
8² = 64	24² = 576
10² = 100	26² = 676
12² = 144	28² = 784
14² = 196	30² = 900
16² = 256

Squares 1 to 30 - Odd Numbers

From numbers 1 to 30 there are a total of 15 odd numbers. As we know, odd numbers can be expressed in the form of 2n + 1, where n = 0,1,2,3,4,5,…

The values of squares 1 to 30 for odd numbers are listed in the table below.

1² = 1	17² = 289
3² = 9	19² = 361
5² = 25	21² = 441
7² = 49	23² = 529
9² = 81	25² = 625
11² = 121	27² = 729
13² = 169	29² = 841
15² = 225

How to Find the Values of Squares for numbers 1 to 30?

There are 2 methods listed below for calculating the values of squares of numbers ranging from 1 to 30.

Method 1: Multiplication by itself:

Under this method, the square's value is determined by multiplying a given number by itself.

For example, the square of 6 = 6 × 6 = 36. Here, the resultant product “36” gives us the square of the number “6.” Generally, this method is applied to smaller numbers.

Method 2: Applying basic algebraic identities:

This method involves first expressing a given number n as (a+b) or (a-b), where "a" stands for a multiple of 10 and "b" stands for any value less than 10. The value of the provided number's squares is then calculated using the basic algebraic formula. (a + b)² = a² + b² + 2ab or (a - b)² = a² + b² - 2ab. This method is used where b has a smaller value.

For example, to find the square of 28, we can express 28 as

Option 1: (20 + 8)
Option 2: (29 - 1)

The basic algebraic identity formula is used in the following step to obtain

Option 1: [20² + 8² + (2 x 20 x 8)] or
Option 2: [29² + 1² - (2 x 29 x 1)].

After expanding the expressions, we get

Option 1: 400 + 64 + 320 = 784
Option 2: 841 + 1 - 58 = 784.