Are you a regular school student who is looking to understand what the square roots of a number are? Or are you a student who is preparing for the various Maths Olympiad exams and struggling to understand the methods of finding square roots of 1 to 30?
If yes, then this blog will be helpful for you. Here we’ll be discussing square roots from 1 to 30. The meaning of square roots, square root chart, table of square roots, methods of finding square roots, solved examples on square roots, etc. are discussed here. So let’s begin!
Meaning of Square Roots
Often students look confused when asked about the definition of square roots, to help out we have provided the definition that students can refer to.
Definition of Square root
The square root of any number is equal to a number that, when squared, yields the original number.
For example, the square root of 16 is 4. If 4 is multiplied by itself, we get 16. [i.e., 4 × 4 = 16].
Thus, the square root of 16 is represented as √16 = 4.
Square roots of any number basically have both values on negative and positive sides. The range of positive square roots from 1 to 30 is 1 to 5.477.
The square roots of 1 to 30 are represented in radical form as √x, where x is a number between 1 to 30. Similar to this, it can be expressed exponentially as (x)1/2, where x = 1 to 30.

Symbol of Square Root
Usually, the symbol for the square root is "√". It's referred to as a radical symbol. This symbol can be used to represent the number 'x' as its square root as follows:
√x where x is the number
The radicand is the number that appears under the radical symbol.
For example, the square root of 25 is also represented as the radical of 25. The value is the same for both.
Formula for Square Roots
The formula to calculate the square root is:
√x = x½
Where, x is the number.
If x is any number such that x = y x y, then the formula to find the square root of x will be
√x = √(y × y) = y
Where, y = square root of any number x.
This indicates that x would be a perfect square if the value of y is an integer.
Square Root Rules
We have some important rules based on operations with square roots.
| Rules | Example |
| √x2 = x | √52 = 5 |
| (√x)2 = x | (√7)2 = 7 |
| √x √y = √xy | √3 √12 = √36 = 6 |
| √x/y = √x/√y | √24/√6 = √24/6 = √4 = 2 |
Here x > 0 and y > 0.

Square Roots Chart
The below charts show the square root values for numbers 1 to 30. Students must learn the square root values for 1 to 30 from charts to enhance computation accuracy and speed. Mastering the concept behind square roots is crucial for preventing errors in complex calculations. Let's start learning the square root values for numbers 1 to 30 which are explained into 3 stages i.e. square roots from 1 to 10, square roots from 11 to 20 and square roots from 21 to 30.
Square Roots 1 to 10
The below chart shows the value of square roots from 1 to 10.

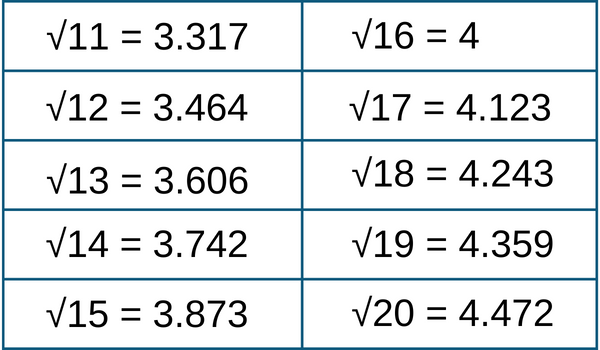
Square Roots 11 to 20
The below chart shows the value of square roots from 11 to 20.
Square Roots 21 to 30
The below chart shows the value of square roots from 21 to 30.

Table of Square Roots
Students will be able to easily simplify the time-consuming long equations by learning the square roots table of 1 to 30. The table below shows the values of square roots from 1 to 30 up to 3 decimal places. Let’s check the square roots list!
| √1 = 1 | √16 = 4 |
| √2 = 1.414 | √17 = 4.123 |
| √3 = 1.732 | √18 = 4.243 |
| √4 = 2 | √19 = 4.359 |
| √5 = 2.236 | √20 = 4.472 |
| √6 = 2.449 | √21 = 4.583 |
| √7 = 2.646 | √22 = 4.690 |
| √8 = 2.82 | √23 = 4.796 |
| √9 = 3 | √24 = 4.899 |
| √10 = 3.162 | √25 = 5 |
| √11 = 3.317 | √26 = 5.099 |
| √12 = 3.464 | √27 = 5.196 |
| √13 = 3.606 | √28 = 5.292 |
| √14 = 3.742 | √29 = 5.385 |
| √15 = 3.873 | √30 = 5.477 |
Students are advised to thoroughly memorize the square root values from 1 to 30 in order to perform mathematical calculations more quickly.

Square Roots for Perfect Squares (For Numbers 1 to 30)
In square roots 1 to 30, the numerals 1, 4, 9, 16 and 25 are perfect squares. The values of square roots from 1 to 30 for perfect squares are listed in table form. Look at the table below to quickly learn the values of square roots from 1 to 30 for perfect squares.
| √1 = 1 | √4 = 2 |
| √9 = 3 | √16 = 4 |
| √25 = 5 |
Square Roots for Non-Perfect Squares (For Numbers 1 to 30)
Except for the numbers 1, 4, 9, 16 and 25, all numbers from 1 to 30 are considered non-perfect square numbers (their square root will be in irrational form).
Look at the table below to quickly learn the values of square roots from 1 to 30 for non-perfect squares.
| √2 = 1.414 | √3 = 1.732 |
| √5 = 2.236 | √6 = 2.449 |
| √7 = 2.646 | √8 = 2.828 |
| √10 = 3.162 | √11 = 3.317 |
| √12 = 3.464 | √13 = 3.606 |
| √14 = 3.742 | √15 = 3.873 |
| √17 = 4.123 | √18 = 4.243 |
| √19 = 4.359 | √20 = 4.472 |
| √21 = 4.583 | √22 = 4.690 |
| √23 = 4.796 | √24 = 4.899 |
| √26 = 5.099 | √27 = 5.196 |
| √28 = 5.292 | √29 = 5.385 |
| √30 = 5.477 |

How to find the Square Root for numbers 1 to 30?
For calculating the square roots of numbers from 1 to 30, there are mainly two methods. Here we’ve discussed these 2 methods of finding square roots for students to learn.
Method 1: Prime Factorization
The prime factorization method can be used to find square roots easily for perfect square numbers like 1, 4, 9, 16, and 25.
Example: Value of √25
Prime factorization of 25 is 5 × 5
Pairing prime factors: 5
Therefore, the value of √25 = 5
Method 2: Finding square roots by long division method
The long division method for finding square roots can be used for non-perfect square numbers like 2, 3, 5, 6, 7, 8, 10, etc.,
Square Roots Tricks
The methods for calculating the square root of perfect squares are simple to remember. We must remember the unit place digit of squares of numbers ranging from 1 to 10.
Refer to the table below for the unit digits we get after squaring a number
| Number (n) | Unit digit of n2 |
| 1 | 1 |
| 2 | 4 |
| 3 | 9 |
| 4 | 6 |
| 5 | 5 |
| 6 | 6 |
| 7 | 9 |
| 8 | 4 |
| 9 | 1 |
| 10 | 0 |
Note: As a result of the above table, we can deduce that if any perfect square ends with the above digits at the unit place, its square root will have the same digits at the unit place.
Examples:
- Square root of 81 is 9
- Square root of 144:
Since it is a three digit number we need to follow a few steps to get the result.
Step 1: Split the digits from the R.H.S as 1 44.
Step 2: The unit place of 144 is 4. As a result, the square root will have either 2 or 8 at the unit place.
Step 3: Using the first digit, 1, calculate the square of 1. As a result, the first digit of 144's square root is 1. Because 1 is the smallest number in the square.
Step 4: Hence, the square root of 144 will take a smaller number between 2 and 8. As a result, it will be 2.
Therefore, the required square root is 12.
Solve and enjoy !!!
- Square root of 169
- Square root of 196
- Square root of 225
Square Roots of Decimal Numbers
A decimal number is a number that includes a decimal point, representing parts of a whole. Square roots of decimal numbers are essentially the numbers that, when multiplied by themselves, result in the given decimal.
For example, the square root of 4.41 is a number that, when multiplied by itself, gives us 4.41. The square root of 4.41 is approximately 2.1 since 2.1 * 2.1 ≈ 4.41.
Methods to Calculate Square Roots of Decimals
Calculating square roots of decimal numbers can be done through various approaches, including the following:
Estimation Method: One of the simplest methods is to estimate the square root using the knowledge of square roots of perfect squares. For instance, to find the square root of 7.29, we can approximate it to the nearest perfect square, which is 2.7 (since √7.29 ≈ 2.7). This method provides a reasonable approximation.
Long Division Method: The Long Division method is a powerful tool to calculate the square root of any given number, including decimal numbers. Let's walk through the step-by-step process with an example of finding the square root of 2.56.
Step 1: To begin, we place a bar over every pair of digits of the decimal number, starting from the unit's place. In this case, we have two pairs: 2 and 56.
Step 2: We start with the whole number part and divide it by the largest number whose square is less than or equal to the whole number. Here, the whole number part is 2 and the largest number whose square is less than or equal to 2 is 1 (since 1 * 1 = 1). So, the quotient is 1.
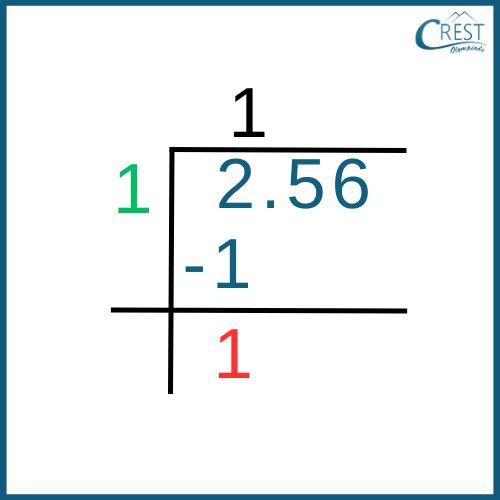
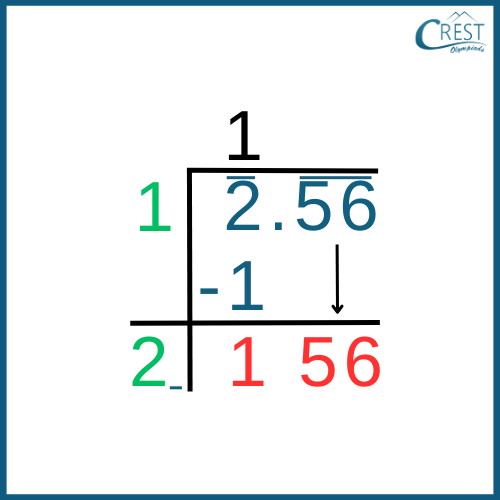
Step 3: Next, we bring down the pair of fractional digits (56) under the next bar to the right of the remainder, which is 1.
Step 4: Now, we add the last digit of the quotient (1) to the divisor, which gives us 1 + 1 = 2. To the right of this sum (2), we find a suitable number that, when multiplied by 2, forms a new divisor for the new dividend (156) that is carried down. We also add a decimal point after 1 in the quotient since we move to the fractional part.
Step 5: The new number in the quotient will have the same number as the one selected in the divisor, which makes the new divisor 26. The quotient is then 1.6 because 26 * 6 = 156 (satisfying the condition of being less than or equal to the dividend).
Step 6: We continue this process further by using the decimal point and adding zeros in pairs to the remainder.
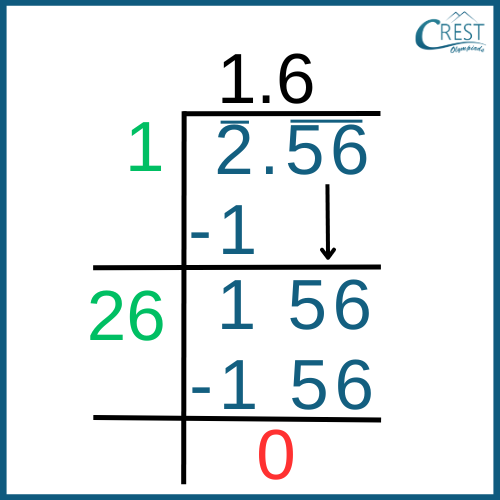
Step 7: The quotient obtained after the required precision will be the square root of the number. In this example, the square root of 2.56 is 1.6.

PDF for Square root values of 1 to 30
Students can access the following link to download the pdf for square root values of 1 to 30.
Download PDF for Square Root Values of 1 to 30
Example Questions for Square Roots of 1 to 30
Example 1: Using the prime factorization method, find the value of 324.
Solution:
By using the prime factorization method,
We get, 324 = 2 x 2 x 3 x 3 x 3 x 3
√324 = √(2 x 2 x 3 x 3 x 3 x 3)
√324 = 2 x 3 x 3 = 18
Therefore, the value of √324 is 18
Example 2: Simplify the expression: 2√4 + 4.
Solution:
Given expression: 2√4 + 4.
We know that √4 = 2.
Substituting the value in the given expression, we obtain
2√4 + 4 = 2(2) + 4
2√4 + 4 = 4 + 4
2√4 + 4 = 8
Therefore, the simplified form of the expression 2√4 + 4 is 8.
Solve!!!
- Square root of 5
- Square root of 8
- Square root of 6
- Square root of 7
- Square root of 25
- Square root of 20
Conclusion
Thus, this was all about square roots 1 to 30 from our end. Hope students understand the square roots of 1 to 30 in a simple way. Students can also practice the problems and compare their answers to those provided by us.
You Might Also Like
- Values of Squares from 1 to 30
- Values of Cubes from 1 to 20
- Tables from 2 to 20
- Multiplication Tables
- Mental Maths Worksheet for Class 1
- Mental Maths Worksheet for Class 2
- Mental Maths Worksheet for Class 3
- Mental Maths Worksheet for Class 4
- Mental Maths Worksheet for Class 5
- Mental Maths Worksheet for Class 6
- Mental Maths Worksheet for Class 7
- Mental Maths Worksheet for Class 8
- Mental Maths Worksheet for Class 9
- Mental Maths Worksheet for Class 10
- Mental Maths Worksheet for Class 11
- Mental Maths Worksheet for Class 12








