Solved Questions on Knowing Our Numbers
1. If p and q are two co-primes, what is their lowest common multiple?
a) q + p
b) q − p
c) q × p
d) q ÷ p
Answer: c) q × p
Explanation: The LCM of the co-prime numbers is the product of these two numbers.
Hence, LCM (p, q) = p × q = q × p
2. Which of the following numbers is divisible by 21?
a) 27604
b) 27804
c) 27894
d) 27904
Answer: b) 27804
Explanation: To divide the number by 21, it must be divisible by 3 and 7.
Divisibility by 3: To check divisibility by 3, find the sum of its digits to check divisibility.
a) Sum of digits of the number 27604
= 2 + 7 + 6 + 0 + 4 = 19, which is not divisible by 3
b) Sum of digits of the number 27804
= 2 + 7 + 8 + 0 + 4 = 21, which is divisible by 3
c) Sum of digits of the number 27894
= 2 + 7 + 8 + 9 + 4 = 30, which is divisible by 3
d) Sum of digits of the number 27904
= 2 + 7 + 9 + 0 + 4 = 22, which is not divisible by 3
Hence, the numbers 27804 and 27894 are divisible by 3.
Divisibility by 7: To check divisibility by 7, double the last digit and subtract the result from the remaining part of the number to check divisibility.
a) 27604: 2760 – (2 × 4) = 2752 which is not divisible by 7.
b) 27804: 2780 – (2 × 4) = 2772 which is divisible by 7.
c) 27894: 2789 – (2 × 4) = 2781 which is not divisible by 7.
d) 27904: 2790 – (2 × 4) = 2782 which is not divisible by 7.
Hence, the number 27804 is divisible by 7.
Therefore, 27804 is divisible by both 3 and 7. Hence, 27804 is divisible by 21.
3. Identify the suitable law for this identity:
5013 × 5031 − 5013 × 5103 = 5013 × (5031 − 5103)
a) Distributive Law of Addition over Multiplication.
b) Distributive Law of Subtraction over Multiplication.
c) Distributive Law of Multiplication over Addition.
d) Distributive Law of Multiplication over Subtraction.
Answer: d) Distributive Law of Multiplication over Subtraction.
Explanation: The distributive law of Multiplication over Subtraction states that:
If A, B and C are three whole numbers, then
A × (B − C) = (A × B) − (A × C)
Hence, the suitable law for this identity is the distributive law of Multiplication over Subtraction.
5013 × (5031 − 5103) = 5013 × 5031 − 5013 × 5103
OR
5013 × 5031 − 5013 × 5103 = 5013 × (5031 − 5103)
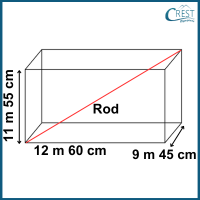
4. The dimensions of a room are 12 m 60 cm, 9 m 45 cm and 11 m 55 cm, respectively. What is the longest rod that can measure precisely three dimensions of a room?
a) 1 m 5 cm
b) 1 m 50 cm
c) 10 m 5 cm
d) 10 m 50 cm
Answer: a) 1 m 5 cm
Explanation: The dimensions of the room are:
Length = 12 m 60 cm = 12 m + 60 cm = (12 × 100) cm + 60 cm = 1260 cm
Breadth = 9 m 45 cm = 9 m + 45 cm = (9 × 100) cm + 45 cm = 945 cm
Height = 11 m 55 cm = 11 m + 55 cm = (11 × 100) cm + 55 cm = 1155 cm
Thus, the longest rod that can measure precisely three dimensions of a room is HCF of 1260, 945 and 1155.
Using prime factorization,
1260 = 2 × 2 × 3 × 3 × 5 × 7
945 = 3 × 3 × 3 × 5 × 7
1155 = 3 × 5 × 7 × 11
HCF (1260, 945, 1155) = 3 × 5 × 7 = 105
Longest rod that can measure the dimensions of the room exactly
HCF (1260, 945, 1155) = 105 cm
= 100 cm + 5 cm
= 1 m 5 cm
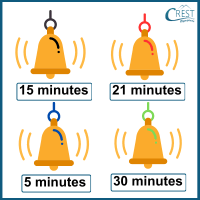
5. Four bells will start tolling together at intervals of 15 minutes, 21 minutes, 5 minutes and 30 minutes, respectively. After how many seconds do they toll together?
a) 12000 seconds
b) 12200 seconds
c) 12400 seconds
d) 12600 seconds
Answer: d) 12600 seconds
Explanation: To find the bells toll together, we should find LCM.
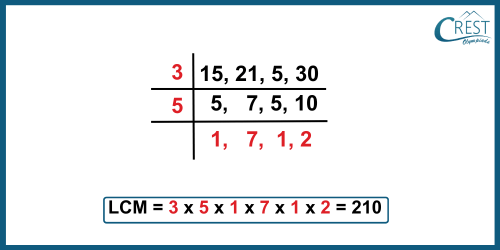
Time after which bells will toll together = LCM (15, 21, 5, 30)
= 210 minutes
= 210 × 60 seconds
= 12600 seconds




