Worksheet on Height and Distance for Class 1

Solved Questions on Height and Distance

1. The angle of elevation of the top of a building from a point on the ground is 45o. If the distance from the point to the building is 50 metres, what is the height of the building?

a) 25 metres
b) 50 metres
c) 75 metres
d) 100 metres

Answer: b) 50 metres

Explanation: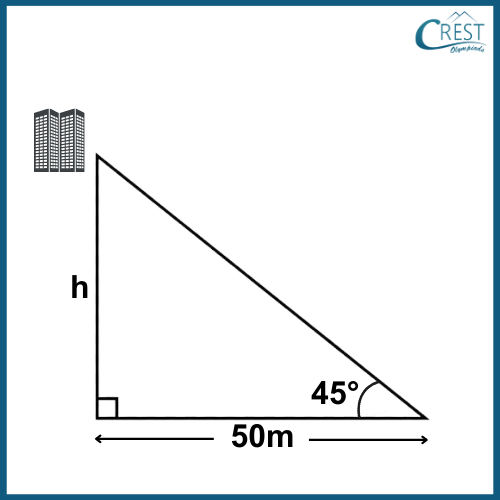

Given: Angle of elevation = 45^o, Distance from point to building = 50 metres

Let the height of the building be h metres.

We can use the tangent function to find the height of the building as follows:
tan (45^o) = h/50
Simplifying the equation, we get:
h = 50 x tan (45^o)
Using the value of tan (45^o) = 1, we get:
h = 50 x 1

Therefore, the height of the building is 50 metres.

2. A 10 metres tall tree is located 20 metres away from a building. The angle of elevation from the top of the tree to the top of the building is 30^o. What is the height of the building?

a) 21.50 m
b) 32.64 m
c) 41.86 m
d) 53.45 m

Answer: a) 21.50 m

Explanation: Given: Height of the tree = 10 metres,
Distance from tree to building = 20 metres,
Angle of elevation = 30^o
Let the height of the building be h metres.
We can use the tangent function to find the height of the building as follows:

tan (30^o) = (h - 10) / 20

Simplifying the equation, we get:
h - 10 = 20 x tan (30^o)
Using the value of tan (30^o) = 1/√3, we get
h - 10 = 20 x (1/√3)
h - 10 = (20/√3)
h = (20/√3) + 10

Simplifying further, we get:
h = (20 + 10√3) / √3
use √3 = 1.74
then, h = (20 + 10 x 1.74) / 1.74

Therefore, the height of the building is approximately 21.50 metres.

3. The angle of depression of a boat from the top of a lighthouse is 60^o. If the height of the lighthouse is 50 metres, what is the distance between the boat and the lighthouse?

a) 9.67metres
b) 11.25 metres
c) 28.87 metres
d) 31.05 metres

Answer: c) 28.87 metres

Explanation: Given: Angle of depression = 60^o, Height of the lighthouse = 50 metres.
Let the distance between the boat and the base of the lighthouse be d metres.
We can use the tangent function to find the distance between the boat and the lighthouse as follows:

tan (60^o) = 50 / d
Simplifying the equation, we get:
d = 50/tan (60^o)
Using the value of tan (60^o) = √3, we get:
d = 50/√3
use √3 = 1.74
then, d = 50/1.74
d = 28.74 metres

Therefore, the distance between the boat and the base of the lighthouse is approximately 28.74 metres.

4. A kite is flying at a height of 60 metres from the ground. The angle of elevation from a point on the ground to the kite is 45^o. What is the distance between the point and the kite?

a) 60 metres
b) 80 metres
c) 100 metres
d) 120 metres

Answer: a) 60 metres

Explanation: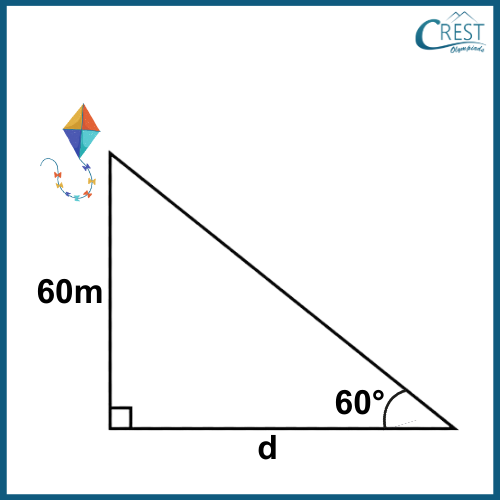

Given: Height of the kite = 60 metres, Angle of elevation = 45^o
Let the distance between the point on the ground and the kite be d metres.

We can use the tangent function to find the distance between the point and the kite as follows:
tan (45^o) = 60 / d
Simplifying the equation, we get:
d = 60 / tan (45^o)
Using the value of tan (45^o) = 1, we get:
d = 60 / 1

Therefore, the distance between the point on the ground and the kite is 60 metres.

5. The angles of elevation of top and bottom of a flag at a distance of 30 m are 45° and 30° respectively. What is the height of the flag AB?

a) 10.54 metres
b) 10 metres
c) 20 metres
d) 12.68 metres

Answers: d) 12.68 m

Explanations: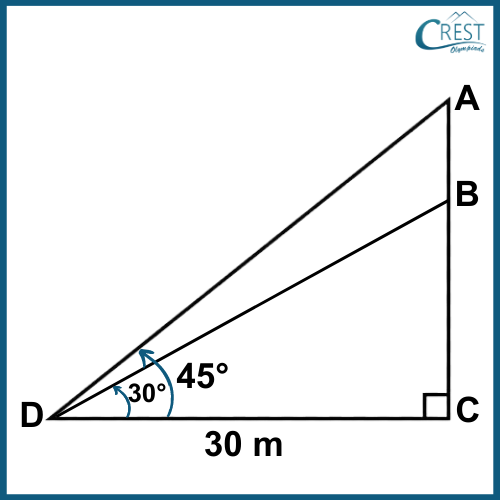

tan 45° = AC/DC
AC = DC tan 45o
= 30 tan 45°
= 30 m
tan 30° = BC/DC
BC = DC tan 30°
BC = 30 tan 30°
= 30 x 1/√3
= 10√3 m

Height of flag AB = 30 - 10√3
= 30 - 17.32
= 12.68 m

Practice Questions on Height and Distance

1. A 15-meter flagpole casts a 15-meter shadow. What is the angle of elevation of the sun?

a) 30^o
b) 45^o
c) 60^o
d) 75^o

Answers: b) 45^o

2. A building is 60 metres tall. From a certain point, the angle of elevation to the top of the building is 30^o. How far is the point from the building?

a) 60√3 metres
b) 45√3 metres
c) 30√3 metres
d) 40√3 metres

Answers: a) 60√3 metres

3. A ladder leans against a wall and makes an angle of 60^o with the ground. If the ladder is 10 metres long, how high up the wall does it reach?

a) 10 metres
b) 9.61 metres
c) 8.7 metres
d) 11.5 metres

Answers: c) 8.7 metres

4. The angle of depression from the top of a 15-metre-tall building to the bottom of a nearby tree is 30^o. What is the distance between the building and the tree?

a) 35 metres
b) 25√3 metres
c) 15 metres
d) 15√3 metres

Answers: d) 15√3 metres

5. The angle of elevation from a point 100 metres away from a tower to the top of the tower is 30^o. What is the height of the tower?

a) 50 metres
b) 57.6 metres
c) 86.6 metres
d) 100 metres

Answers: b) 57.6 metres

6. A tree casts a shadow 12 metres long. At the same time, a 5-metre tall pole nearby casts a shadow 3 metres long. What is the height of the tree?

a) 15 metres
b) 20 metres
c) 25 metres
d) 30 metres

Answers: b) 20 metres

7. A flagpole 21/√3 metres tall casts a shadow 7 metres long. What is the angle of elevation of the sun?

a) 30^o
b) 45^o
c) 60^o
d) 75^o

Answers: c) 60^o

8. The angle of elevation of a balloon from a point on the ground is 30^o. If the balloon is 150 metres above the ground, how far is it from the point on the ground?

a) 154.4 metres
b) 259.5 metres
c) 352.3 metres
d) 473.2 metres

Answers: b) 259.5 metres

9. A plane is flying at an altitude of 10,000 metres. If the angle of elevation to the plane from a point on the ground is 30^o, how far away is the plane from the point on the ground?

a) 5,000 metres
b) 10,000 metres
c) 11,547 metres
d) 20,000 metres

Answers: d) 20,000 metres

10. A cliff is 100 meters high. The angle of depression of a boat in the water at the base of the cliff is 45^o. What is the distance between the boat and the top of the cliff?

a) 70.7 meters
b) 100 meters
c) 141.4 meters
d) 200 meters

Answers: c) 141.4 metres