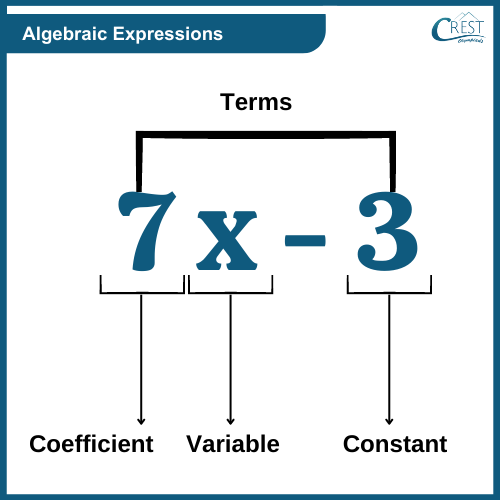
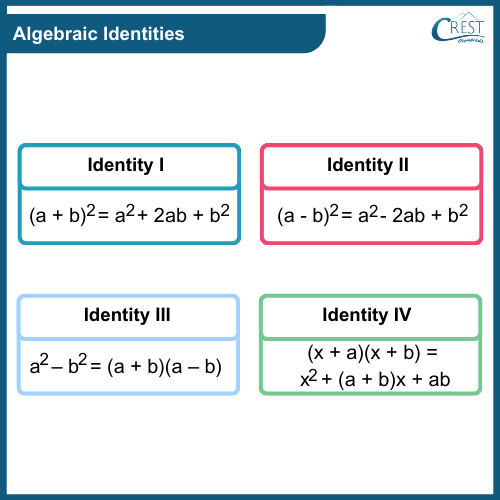
-
Olympiads
- CREST Mathematics Olympiad (CMO)
- CREST Science Olympiad (CSO)
- CREST English Olympiad (CEO)
- CREST Reasoning Olympiad (CRO)
- CREST Cyber Olympiad (CCO)
- CREST Mental Maths Olympiad (CMMO)
- International Green Warrior Olympiad (IGWO)
- CREST International Drawing Olympiad (CIDO)
- CREST International Spell Bee Summer (CSB)
- CREST International Spell Bee Winter (CSBW)
- International Teacher Olympiads
- Class wise
- FAQs
- Student Connect
- Preparation
- Free Trial
- School Registration
- Become a Coordinator
- Explore More
Olympiad Exam Registration Started for 2025-26 | Check 2025-26 Olympiad Exam Dates | Join our WhatsApp Channel for Exam Updates | Buy 2025-26 Olympiad books here | Download Free Maths Olympiad Printable Worksheets | Download Free Science Olympiad Printable Worksheets | Download Free English Olympiad Printable Worksheets |
Check Previous Years Papers